UNIDAD 1: FUNCIONES

1.1 DEFINICIÓN Y NOTACIÓN DE FUNCIÓN

Definición

La definición general de función hace referencia a la dependencia entre los elementos de dos

conjuntos dados.

Dados dos conjuntos A y B, una función (también aplicación o mapeo) entre ellos es una asociación ⁶ f que a cada elemento de A le asigna un único elemento de B.

Se dice entonces que A es el dominio (también conjunto de partida o conjunto inicial) de f y que B es su codominio (también conjunto de llegada o conjunto final).

Un objeto o valor genérico a en el dominio A se denomina la variable independiente; y un objeto genérico b del dominio B es la variable dependiente. También se les llama valores de entrada y de salida, respectivamente. Esta definición es precisa, aunque en matemáticas se utiliza una definición formal más rigurosa, que construye las funciones como un objeto concreto.

Ejemplos

Todos los números reales tienen un cubo, por lo que existe la función «cubo» que a cada número en el dominio R le asigna su cubo en el codominio R.
Exceptuando al 0, todos los números reales tienen un único inverso. Existe entonces la función «inverso» cuyo dominio son los números reales no nulos R \ {0}, y con codominio R.
Cada mamífero conocido se clasifica en un género, como Homo, Sus o Loxodonta. Existe por tanto una función «clasificación en géneros» que asigna a cada mamífero de la colección M = {mamíferos conocidos} su género. El codominio de «clasificación en géneros» es la colección G = {géneros de Mammalia}.
Existe una función «área» que a cada triángulo del plano (en la colección T de todos ellos, su dominio), le asigna su área, un número real, luego su codominio es R.
En unas elecciones en las que cada votante pueda emitir un único voto, existe una función «voto» que asigna a cada elector el partido que elija. En la imagen se muestra un conjunto de electores E y un conjunto de partidos P, y una función entre ellos.

Notación de la función

Cuadro 1: Diagrama de la notación de la función

La notación de la función es una manera de escribir funcionesque aclara el nombre de la función, de las variables independientes, de las variables dependientes, y de la regla de la transformación.

En el ejemplo a la derecha, `f(x)` es la variable dependiente, `f` es el nombre de función, `x` es la variable independiente, y `3x + 2` es la regla de la transformación.

https://www.youtube.com/watch?v=9kAvdvkpmMI

1.2 DOMINO Y RANGO

Hay nombres especiales para lo que puede entrar, y también lo que puede salir de una función:

	Lo que puede entrar en una función se llama el dominio
	Lo que es posible que salga de una función se llama el codominio
	Lo que en realidad sale de una función se llama rango o imagen

Entonces, en el diagrama de arriba el conjunto "X" es el dominio, el conjunto "Y" es el codominio, y los elementos de Y a los que llegan flechas (los valores producidos realmente por la función) son el rango.

Parte de la función

Lo que sale (el rango) depende de lo que pones (el dominio), pero TÚ defines el dominio.

De hecho el dominio es una parte esencial de la función. Un dominio diferente da una función diferente.

Ejemplo: una simple función como f(x) = x² puede tener dominio (lo que entra) los números de contar {1,2,3,...}, y el rango será entonces el conjunto {1,4,9,...}

Y otra función g(x) = x² puede tener como dominio los enteros {...,-3,-2,-1,0,1,2,3,...}, entonces el rango será el conjunto {0,1,4,9,...}

	Aunque las dos funciones toman la entrada y la elevan al cuadrado, operan en conjuntos diferentes de entradas, y por eso dan salidas diferentes.

	También tienen diferentes propiedades. Por ejemplo f(x) siempre da resultados distintos, pero g(x) puede dar la misma respuesta para dos entradas (como g(-2)=4 y g(2)=4)

Así que el dominio es una parte muy importante de la función.

Entonces, ¿todas las funciones tienen su dominio?

Sí, pero en matemáticas sencillas no lo notas, porque el dominio se supone:

Normalmente se supone que es algo así como "todos los números que hacen que funcione".
O si estás estudiando números enteros, el dominio será los enteros.
etc.

¡Pero en matemáticas más avanzadas tienes que tener cuidado!

Codominio y rango

El codominio y el rango tienen que ver con la salida, pero no son exactamente lo mismo.

El codominio es el conjunto de valores que podrían salir.

El rango es el conjunto de valores que realmente salen.

Ejemplo: puedes definir una función f(x)=2x con dominio y codominio los enteros (porque tú lo eliges así).

Pero si lo piensas, verás que el rango (los valores que salen de verdad) son sólo los enteros pares.

Así que el codominio son los enteros (lo has elegido tú) pero el rango son los enteros pares.

Así que rango es un subconjunto del codominio.

¿Por qué los dos? Bueno, a veces no conoces exactamente el rango (porque la función es complicada o no es conocida del todo), pero sabes el conjunto en el que está (como los enteros o los reales). Así que defines el codominio y sigues trabajando.

La importancia del codominio

Déjame que te haga una pregunta: ¿la raíz cuadrada es una función?

Si tú dices que el codominio (las salidas posibles) es el conjunto de los números reales, ¡entonces la raíz cuadrada no es una función! ... ¿te sorprende?

La razón es que podría haber dos respuestas para una entrada, por ejemplo f(9) = 3 o -3

Una función debe ser univaluada. No puede dar 2 resultados para el mismo valor de entrada. ¡Por ejemplo "f(2) = 7 o 9" no está bien!

Pero se puede arreglar simplemente limitando el codominio a los números reales no negativos.

√De hecho, el símbolo radical (como en √x) siempre significa la raíz cuadrada positiva (la principal), así que √x es una función porque su codominio es correcto.

Así que el codominio

Notación

que elijas puede afectar el que algo sea o no una función.

A los matemáticos no les gusta escribir muchas palabras cuando unos pocos símbolos hacen el mismo trabajo. Así que hay maneras de decir que "el dominio es", "el codominio es", etc.

Esta es la mejor manera que conozco:

	Esto dice que la función "f" tiene dominio "N" (los números naturales), y también codominio "N".
	y esto dice que la función "f" toma "x" y devuelve "x²"

https://www.youtube.com/watch?v=28XUF4hRqg8

1.3 Tipos de funciones

Clasificación de funciones

Funciones algebraicas

En las funciones algebraicas las operaciones que hay que efectuar con la variable
independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

Las funciones algebraicas pueden ser:

Funciones explícitas

Si se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x − 2

Funciones implícitas

Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar
operaciones.
5x − y − 2 = 0

Funciones polinómicas

Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn
Su dominio es , es decir, cualquier número real.

Funciones constantes

El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.

Funciones polinómica de primer grado

f(x) = mx +n
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.

Las principales son:

Función afín.
Función lineal.
Función identidad.
Funciones cuadráticas

f(x) = ax² + bx +c
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

Funciones a trozos

Son funciones definidas por distintos criterios, según los intervalos que se consideren.

Funciones en valor absoluto.
Función parte entera de x.
Función mantisa.
Función signo

Funciones racionales

El criterio viene dado por un cociente entre polinomios:3
El dominio lo forman todos los números reales excepto los valores de x que anulan el
denominador.

Funciones radicales

El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.

Funciones trascendentes

La variable independiente figura como exponente, o como índice de la raíz, o se halla
afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

Función exponencial

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.

Funciones logarítmicas

La función logarítmica en base a es la función inversa de la exponencial en base a.

Funciones trigonométricas

Función seno

f(x) = sen x

Función coseno

f(x) = cos x

Función tangente

f(x) = tg x

Función cosecante

f(x) = cosec x4

Función secante

f(x) = sec x

Función cotangente

f(x) = cotg x

Funciones constantes

La función constante es del tipo:
y = n
El criterio viene dado por un número real.
La pendiente es 0.
La gráfica es una recta horizontal paralela a al eje de abscisas.

Rectas verticales

Las rectas paralelas al eje de ordenadas no son funciones, ya que un valor de x tiene infinitas imágenes y para que sea función sólo puede tener una. Son del tipo:
x = K5

Función lineal

La función lineal es del tipo:
y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.

y = 2x

x 0 1 2 3 4

y = 2x 0 2 4 6 8

Pendiente

m es la pendiente de la recta.

La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.6

Si m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.

Función identidad

f(x) = x
Su gráfica es la bisectriz del primer y tercer cuadrante.

Función afín

La función afín es del tipo:
y = mx + n
m es la pendiente de la recta.

La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Dos rectas paralelas tienen la misma pendiente.

n es la ordenada en el origen y nos indica el punto de corte de la recta con el eje de
ordenadas.

Ejemplos de funciones afines

Representa las funciones:
1 y = 2x - 1
x y = 2x-1
0 -1
1 1

2y = -¾x - 1
x y = -¾x-1
0 -1
4 -4

Función cuadrática

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
f(x) = ax² + bx +c

Representación gráfica de la parábola

Podemos construir una parábola a partir de estos puntos:
1. Vértice
Por el vértice pasa el eje de simetría de la parábola.
La ecuación del eje de simetría es:

2. Puntos de corte con el eje OX
En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:
ax² + bx +c = 0

Resolviendo la ecuación podemos obtener:

Dos puntos de corte: (x1, 0) y (x2, 0) si b² − 4ac > 0
Un punto de corte: (x1, 0) si b² − 4ac = 0
Ningún punto de corte si b² − 4ac < 0 9

3. Punto de corte con el eje OY
En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:
f(0) = a · 0² + b · 0 + c = c (0,c)

Ejemplos:
Representar la función f(x) = x² − 4x + 3.
1. Vértice
x v = − (−4) / 2 = 2 y v = 2² − 4· 2 + 3 = −1
V(2, −1)

2. Puntos de corte con el eje OX
x² − 4x + 3 = 0

(3, 0) (1, 0)

3. Punto de corte con el eje OY
(0, 3)10

Funciones racionales

El criterio viene dado por un cociente entre polinomios:
El dominio lo forman todos los números reales excepto los valores de x que anulan el
denominador.
Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:
. 14
Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones.

Funciones definidas a trozos

Son funciones definidas por distintos criterios, según los intervalos que se consideren.

El dominio lo forman todos los números reales menos el 4.

Función parte entera de x

Es una función que a cada número real hace corresponder el número entero

inmediatamente inferior.

f(x) = E (x)

x 0 0.5 0.9 1 1.5 1.9 2

f(x) = E(x) 0 0 0 1 1 1 2

Función mantisa

Función que hace corresponder a cada número el mismo número menos su parte entera.

f(x) = x - E (x)
x 0 0.5 0.9 1 1.5 1.9 2
f(x) = x - E(x) 0 0.5 0.9 0 0.5 0.9 0

Función exponencial

La función exponencial es del tipo:
Sea a un número real positivo. La función que a cada número real x le hace corresponder
la potencia ax se llama función exponencial de base a y exponente x. 27

Propiedades de la función exponencial
Dominio: .
Recorrido: .
Es continua.
Los puntos (0, 1) y (1, a) pertenecen a la gráfica.
Es inyectiva a ≠ 1(ninguna imagen tiene más de un original).
Creciente si a >1.
Decreciente si a < 1.
Las curvas y = ax e y = (1/a)x son simétricas respecto del eje OY.

1.4 OPERACIONES CON FUNCIONES

Suma de funciones

(f + g)(x) = f(x) + g(x)

Dominio

D(f + g) = D f D g

Ejemplo

D_f =

− {2}D_g = [0, ∞)

D(f + g) = [0, 2) unión

(2, ∞)

Propiedades

Asociativa:

f(x) + [g(x) + h(x)] = [f(x) + g(x)] + h(x)

Conmutativa:

f(x) + g(x) = g(x) + f(x)

Elemento neutro:

La función constante: f(x) = 0.

Elemento simétrico:

La función opuesta: −f(x).

Resta de funciones

(f − g)(x) = f(x) − g(x)

Dominio

D(f − g) = D f D g

D(f + g) = [0, 2) unión

(2, ∞)

Producto de funciones

(f · g)(x) = f(x) · g(x)

Dominio

D(f · g) = D f D g

D(f + g) = [0, 2) unión

(2, ∞)

Propiedades

Asociativa:

f(x) · [g(x) · h(x)] = [f(x) · g(x)] · h(x)

Conmutativa:

f(x) · g(x) = g(x) · f(x)

Elemento neutro:

La función constante: f(x) = 1.

Distributiva:

f(x) · [g(x) + h(x)] = [f(x) · g(x)] + [f(x) · h(x)]

División de funciones

(f / g)(x) = f(x) / g(x)

Dominio

D(f + g) =(D f D g) − {x / g(x) = 0}

D f =

− {2}D g = [0, ∞) g(x) ≠ 0

D(f + g) = (0, 2) unión

(2, ∞)

https://www.youtube.com/watch?v=78QxHDCibIE

1.5 COMPOSICIÓN DE FUNCIONES

Dadas dos funciones reales de variable real, f y g, se llama composición de las

funciones f y g, y se escribe g o f, a la función definida de R en R, por (g o f )(x) = g[f(x)].

La función ( g o f )(x) se lee « f compuesto con g aplicado a x ».

Primero actúa la función f y después actúa la función g, sobre f(x).

Cálculo de la imagen de un elemento mediante una función compuesta

Para obtener la imagen de la función compuesta aplicada a un número x, se siguen estos pasos:

1. Se calcula la imagen de x mediante la función f, f(x).

2. Se calcula la imagen mediante la función g, de f(x). Es decir, se aplica la función g al resultado obtenido anteriormente.

Ejercicio:

 Sean las funciones f(x) = x + 3 y g(x) = x².

Calcular g o f y la imagen mediante esta función de 1, 0 y -3.

Resolución:

· La imagen de dos números 1, 0, -3, mediante la función g o f es:

‚ Dadas las funciones f(x) = x² + 1, y g(x) = 3x - 2, calcular:

a) (g o f ) (x)

b) (f o g ) (x)

c) (g o f ) (1) y (f o g ) (-1)

d ) El original de 49 para la función g o f.

Resolución:

c) Aplicando los resultados de los apartados anteriores:

(g o f ) (x) = 3x² + 1 = 49. Basta con resolver esta ecuación.

https://www.youtube.com/watch?v=2Nj5oegrRDs

1.6 Gráfica de una función

En un sistema de coordenadas cartesianas se han representado las curvasde algunas raíces, así como de suspotencias, en el intervalo [0,1]. La diagonal, de ecuación y = x, es eje de simetría entre cada curva y la curva de su inversa.

En matemáticas, la gráfica de una función:

$\begin{array}{rccl} f: & X & \longrightarrow & Y \\ & x & \longmapsto & y= f(x) \end{array}$

Es el conjunto formado por todos los pares ordenados (x, f(x)) de la función f, es decir, como un subconjunto del producto cartesiano X×Y. Se representa gráficamente mediante unacorrespondencia entre los elementos delconjunto dominio y los del conjunto imagen.

Las únicas funciones que se pueden trazar de forma completa son las de una sola variable, con un sistema de coordenadas cartesianas, donde cada abscisa representa un valor de la variable del dominio y cada ordenada representa el valor correspondiente del conjunto imagen. Si la función es continua, entonces la gráfica formará una línea recta ocurva.

En el caso de funciones de dos variables es posible visualizarlas de forma unívoca mediante una proyección geométrica, pero a partir de tres variables tan solo es posible visualizar cortes (con un plano) de la función para los que los valores de todas las variables, excepto dos, permanezcan constantes.

El concepto de gráfica de una función se generaliza a la gráfica de una relación. Notar que si bien cada función tiene una única representación gráfica, pueden existir varias funciones que tengan la misma, pero con dominios y codominios diferentes.

Dominio de definición

El Dominio de definición D de una función es el subconjunto de X que tienen imagen en Y:

$D \subset X \; | \quad \forall x \in D: \; \exists y \in Y \quad \land \quad y= f(x)$

Sin pérdida de la generalidad, consideramos, tanto el conjunto X como Y sea el de los números reales R, siendo X un intervalo o la unión de varios intervalos, podemos diferenciándose los siguientes casos:

El dominio un intervalo abierto: (a,b). Se puede expresar:

$D = \big \{ x \in \R \quad \land \quad a < x < b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor que x y x menor deb, tal que existe y número real é y= f(x).

La forma de representar el intervalo abierto, da lugar a la expresión:

$D = \big \{ x \in \R \quad \land \quad x \in (a, b) \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo abierto (a,b) , tal que existe y número real é y= f(x).

Si el dominio un intervalo semiabierto: (a,b]. Tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad a < x \leq b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor o igual que x y xmenor de b, tal que existe y número real é y= f(x).

Tomando la forma de representar un intervalo semiabierto, tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad x \in (a, b] \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo semiabierto [a,b) , tal que existe y número real é y= f(x).

Si el dominio es el intervalo semiabierto: [a,b). Tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad a \leq x < b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor que x y x menor o igual que b, tal que existe y número real é y= f(x).

Tomando la forma de representar un intervalo semiabierto, tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad x \in [a, b) \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo semiabierto [a,b) , tal que existe y número real é y= f(x).

Si el dominio un intervalo cerrado: [a,b] la expresión resultante es:

$D = \big \{ x \in \R \quad \land \quad a \leq x \leq b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor o igual que x y xmenor o igual que b, tal que existe y número real é y= f(x).

Tomando la forma de representar un intervalo cerrado, tenemos que:

$D = \big \{ x \in \R \quad \land \quad x \in [a, b] \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo cerrado [a,b] , tal que existe y número real é y= f(x).

En estos ejemplos hemos podido ver, las distintas formas de representar los distintos tipos de intervalos, tanto abiertos semiabiertos o cerrados, en una expresión o en una gráfica.

Puntos de discontinuidad

En los puntos extremos de cada intervalo de definición de la función, o en los puntos intermedios de los intervalos de existencia, que presenten discuntinuidad, se presenta un punto de discontinuidad, que puede ser de alguno de estos tipos:

$\mbox{Discontinuidad} { \color{Red} \left \{ \begin{array}{l} \mbox{Evitable} \\ \mbox{Esencial} { \color{PineGreen} \left \{ \begin{array}{l} \mbox{De primera especie} { \color{Blue} \left \{ \begin{array}{l} \mbox{De salto finito} \\ \mbox{De salto infinito} \\ \mbox{Asintótica} \end{array} \right . }\\ \\ \mbox{De segunda especie} \end{array} \right . } \\ \end{array} \right . }$

Galería de discontinuidades


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = \infty \\ \\ \nexists \; \underset{x \to {a}^{+}}{\lim} \; f(x) \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = -\infty \\ \\ \nexists \; \underset{x \to {a}^{+}}{\lim} \; f(x) \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \nexists \; \underset{x \to {a}^{+}}{\lim} \; f(x) \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \nexists \; \underset{x \to {a}^{+}}{\lim} \; f(x) \\ \\ f(a) = L \end{array} \right .$
De segunda especie.	De segunda especie.	De segunda especie.	De segunda especie.


$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{\lim} \; f(x) \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{\lim} \; f(x) \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = -\infty \end{array} \right .$	$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{\lim} \; f(x) \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \end{array} \right .$	$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{\lim} \; f(x) \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \\ \\ f(a) = L \end{array} \right .$
De segunda especie.	De segunda especie.	De segunda especie.	De segunda especie.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = -\infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = -\infty \end{array} \right .$
Asintótica.	Asintótica.	Asintótica.	Asintótica.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = \infty \\ \\ f(a) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = -\infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = -\infty \\ \\ f(a) = L \end{array} \right .$
De salto infinito.	De salto infinito.	De salto infinito.	De salto infinito.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \\ \\ f(a) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \\ \\ f(a) = L \end{array} \right .$
De salto infinito.	De salto infinito.	De salto infinito.	De salto infinito.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L1 \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L2 \\ \\ L1 \ne L2 \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L1 \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L2 \\ \\ L1 \ne L2 \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L1 \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L2 \\ \\ L1 \ne L2 \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{\lim} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{\lim} \; f(x) = L \\ \\ \nexists \; f(a) \end{array} \right .$
De salto finito.	De salto finito.	De salto finito.	Evitable

Ejemplos

Gráfica de la función x³-9x.

La gráfica de la función

$f(x)=\left\{\begin{matrix} a, & \mbox{si }x=1 \\ b, & \mbox{si }x=2 \\ c, & \mbox{si }x=3. \end{matrix}\right.$

es {(1,a), (2,b), (3,c)}.

La gráfica del polinomio cúbico en la recta real

$f(x)={{x^3}-9x} \!\$

es {(x,x³-9x) : donde x es un número real}. Si el conjunto se representa en un plano cartesiano, el resultado es como el de la imagen.

Método para representar la gráfica de una función de una variable

Una función con una variable dependiente y otra independiente se puede representar gráficamente en un eje de ordenadas y abscisas correspondiendo el valor de cada variable a la posición en los ejes. Normalmente se utiliza la variable $\,x$ para el eje de abscisas y la variable $\,y$ para el eje de ordenadas.

Para dibujar, construir o representar la gráfica de una función f se pueden seguir los pasos siguientes:

Buscar el dominio de la función, Dom f(x)
Se detectan aquellos valores x reales en que f sea discontinua, es decir, aquellos que no estén definidos en el dominio, y se procede a estudiar los límites cuando xtiene a x por la izquierda y por la derecha. De este modo, si x es un punto aislado y no un intervalo, se puede deducir hacia dónde tiende la función cuando pasa cerca del punto x.
Buscar los límites cuando x tiende a infinito o menos infinito, para averiguar cuándo en el eje de abscisas se tiende al resultado del límite.
Estudio de la monotonía. Calculando la primera derivada f'(x) e igualándola a cero, se obtienen los posibles candidatos a extremos de la función. Luego se procede a determinar si f(x) es creciente o decreciente entre dos puntos extremos.
Se estudia la curvatura de f, igualando a cero esta vez la segunda derivada f(x), obteniéndose los posibles puntos de inflexión. Se estudia el signo en la f(x) en los intervalos, y así, sea x uno de estos puntos:

Si f(x) es negativa, entonces f(x) es cóncava

Si f(x) es positiva, entonces f(x) es convexa.

Las funciones lineales y cuadráticas se pueden escribir de la forma f(x) = mx + b, y f(x) = ax2 + bx + c respectivamente, quieres saber a detalle que son las funciones lineales y cuadráticas, cómo se representan en la gráfica y algunos ejemplos? Sigue leyendo!

Funciones lineales y cuadráticas

Funciones lineales

Una función lineal es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.

Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.

m = pendiente de la recta (constante).

b = punto de corte de la recta con el eje y (constante).

x = variable.

Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.

Las funciones se pueden clasificar en tres tipos:

Si el valor de “m” es mayor a cero la función es creciente.
Si el valor de “m” es menor a cero la función es decreciente.
Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).

Estos son los tres tipos de funciones:

Haz click en la imagen para verla más grande

Ejemplo

Tenemos la siguiente función: y = 1.5 x + 3

la pendiente es 3/2, cuando aumentamos x en una unidad “y” aumenta en 3/2 de unidad, b = 3 entonces la recta corta el eje y en el punto y = 3.

Para graficar podemos hacer una tabla de valores y graficamos cada punto en el plano cartesiano.

Funciones cuadráticas

Una función cuadrática es una función polinómica de segundo grado que se escribe : f(x) = ax2 + bx + c

a, b y c = números reales diferentes a cero.

Si a>0 el vértice de la parábola estará en la parte inferior y si o a<0 el vértice estará en la parte superior de la parábola.

La gráfica de una función cuadrática es una parábola de la cual el eje de simetría es paralelo al eye de las “y”.

Modificaciones en la función, si sumamos o restamos dentro del paréntesis la parábola se mueve hacia la izquierda o la derecha respectivamente, Si restamos o sumamos en la función fuera del paréntesis la parábola se mueve hacia abajo o hacia arriba.

Para obtener la raíces de la ecuación seguimos estos pasos:

Igualar la ecuación a cero.
Factorizar la ecuación.
Igualar cada factor a cero y obtener las raíces.

Para graficar la función seguimos estos pasos:

Con el valor de “a” determinar si la parábola abre hacía arriba o hacía abajo.
Obtener los puntos de intersección, los del eje “x” se obtienen con las raíces de la ecuación, para obtener las intersecciones en “y” igualamos la x a cero.
Obtener el vértice de la función, el punto “x” de la coordenada del vértice se obtiene con la fórmula -b/2a y el punto “y” se obtiene sustituyendo x en la función.
Graficar los puntos obtenidos en los puntos 2 y 3 para graficar la curva.

- See more at: http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/#sthash.LyHwFHx1.dpuf

www.youtube.com/watch?v=E5cQtFEHI6I

1.8 FUNCIÓN EXPONENCIAL Y LOGARÍTMICA

Función exponencial

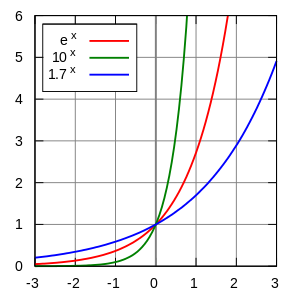
Funciones exponenciales
Gráfica de Funciones exponenciales
Definición	$e^x , \exp(x)\,$
Tipo	Función real
Dominio	$(-\infty,+\infty)$
Codominio	$(0,+\infty)$
Imagen	$(0,+\infty)$
Propiedades	Biyectiva Convexa Estrictamente creciente Trascendente
Cálculo infinitesimal
Derivada	$e^x \,$
Función primitiva	$e^x \,$
Función inversa	$\ln(x)\,$
Límites	$\lim_{x\to -\infty}\exp(x)= 0\,$ $\lim_{x\to+\infty}\exp(x)=+\infty\,$
Funciones relacionadas	Logaritmo
[editar datos en Wikidata]

La función exponencial, es conocida formalmente como la función real e^x, dondee es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que suderivada es la misma función. Se denota equivalentemente como f(x)=e^x o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma

$E(x)=K \cdot a^x$

siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.

Definición formal

La función exponencial e^x puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:

$e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \ldots$

o como el límite de la sucesión:

$e^x = \lim_{n \to \infty} \left( 1 + {x \over n} \right)^n$

Propiedades[editar]

La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.

Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)

$\exp(x+y) = \exp(x) \cdot \exp(y)$

$\exp(x-y) = \exp(x) / \exp(y) \,$

$\exp(-x) = {1 \over \exp(x)}$

$\exp(0) = 1 \,$

¿Qué es un logaritmo?

Es la función inversa de la función exponencial de base a, de manera que el numero y tal que ay = x, recibe el nombre de logaritmo, en base a del numero x.
Se expresa:

La igualdad anterior, nos permite calcular algunos logaritmos de manera immediata. Por ejemplo:

Concepto de la funcion logarítmica

Propiedades

El logoritmo de un producto es igual a la suma de los logaritmos de los factores:

El logaritmo de una división es igual a la resta de logaritmos:

El logaritmo de una poténcia es igual al exponente multiplicado por el logaritmo de la base de la poténcia:

El logaritmo de un radical es igual al exponente dividiendo al logaritmo:

A continuacion os ofrecemos un video en el cual explica estas propiedades y algunas otras que resultan interesantes. Para ver el video pulse aqui.

Cambio de base

Se puede llevar a cabo el cambio de base siguiendo la relación siguiente:

Otras propiedades

Tiene límites infinitos en 0+ i +.
El limite de cualquier logaritmo de numero 1 es igual a 0:

donde a es cualquier numero.

Un logaritmo de la misma base y del mismo numero es igual a 1:

www.youtube.com/watch?v=NDYtaTWa8Mk

1.9 Las Funciones y sus Aplicaciones a la Administración y Economía

Curvas de Oferta y Demanda Lineales En la práctica, algunas ecuaciones de oferta y demanda son aproximadamente lineales en el intervalo que importa. Otras son no lineales.
3 Aún en estos últimos casos, las ecuaciones lineales suelen proporcionar representaciones razonablemente precisas de la oferta y la demanda en un intervalo limitado. En general, las ecuaciones de oferta y demanda lineales se utilizan para mayor simplicidad y claridad al ilustrar ciertos tipos de análisis.
4. 4 precioEn la práctica, una representación general de las curvas de oferta y demanda es la siguiente: cantidad demandada q p O D

Resultado de imagen para CURVA oferta y demanda grafica

5. 5 En este caso, en cambio, se representa la oferta y a la demanda como funciones lineales. precio cantidad demandada q p O D
6. 6 Debe notarse, eso sí, que sólo los segmentos de las ecuaciones que estén en el primer cuadrante son pertinentes al análisis económico. Esto ocurre porque oferta, precio y cantidad son, en general, cero o positivas.
7. 7 Por ejemplo, en formas más simples del análisis económico: • Una oferta negativa, implica que los bienes no se pueden obtener en el mercado, sea porque no se producen o porque se retienen hasta que se ofrezca un precio satisfactorio. pprecio cantidad demandada q O Oferta negativa
8. 8 Un precio negativo, implica que se paga a los compradores para que se lleven los males del mercado. precio cantidad demandada q p precio negativo
9. 9 Una cantidad demandada negativa, implica que los precios son tan altos como para impedir la actividad del mercado hasta que se ofrezcan cantidades a precios satisfactorios. precio cantidad demandada q p cantidad demandada negativa
10. 10 Estos casos pueden ocurrir, pero su incidencia es poco frecuente y sólo se consideran en análisis económico más avanzado.
11. 11 Curvas de demanda lineales En el caso común, la pendiente de una curva de demanda es negativa, es decir, a medida que el precio aumenta, la cantidad demandada decrece y viceversa. precio cantidad demandada q p p1 p2 q1q2
12. 12 En algunos casos, la pendiente de una curva de demanda puede ser cero: precio constante sin considerar la demanda. precio cantidad demandada
13. 13 En otros casos la pendiente puede no estar definida: demanda constante sin importar el precio. precio cantidad demandada

MATEMATICAS

domingo, 24 de mayo de 2015

UNIDAD 1: FUNCIONES

UNIDAD 1: FUNCIONES

1.1 DEFINICIÓN Y NOTACIÓN DE FUNCIÓN

Definición

1.2 DOMINO Y RANGO

Parte de la función

Entonces, ¿todas las funciones tienen su dominio?

Codominio y rango

La importancia del codominio

Notación

1.3 Tipos de funciones

Clasificación de funciones

Funciones algebraicas

Funciones explícitas

Funciones implícitas

Funciones polinómicas

Funciones constantes

Funciones polinómica de primer grado

Funciones a trozos

1.4 OPERACIONES CON FUNCIONES

Suma de funciones

Dominio

Ejemplo

Propiedades

Resta de funciones

Dominio

Producto de funciones

Dominio

Propiedades

División de funciones

Dominio

1.5 COMPOSICIÓN DE FUNCIONES

1.6 Gráfica de una función

Dominio de definición

Puntos de discontinuidad

Galería de discontinuidades

Ejemplos

Método para representar la gráfica de una función de una variable

Funciones lineales y cuadráticas

Funciones lineales

Ejemplo

Funciones cuadráticas

1.8 FUNCIÓN EXPONENCIAL Y LOGARÍTMICA

Función exponencial

Definición formal

Propiedades[editar]

Funciones logarítmicas

Propiedades

Cambio de base

Otras propiedades

1.9 Las Funciones y sus Aplicaciones a la Administración y Economía

No hay comentarios:

Publicar un comentario