UNIDAD ll. LIMITES Y CONTINUIDAD
2.1 Definición de Límite
En matemática, el concepto de límite es una noción topológica que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.
En cálculo infinitesimal (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación,integración, entre otros. Si bien, el concepto de límite parece intuitivamente relacionado con el concepto de distancia, en un espacio euclídeo, es la clase de conjuntos abiertosinducidos por dicha métrica, lo que permite definir rigurosamente la noción de límite.
El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.
Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(an) = a o se representa mediante la flecha (→) como en an → a.
2.2 Propiedades De Los Limites
Los límites forman una parte fundamental del cálculo en las Matemáticas. De hecho, el primer punto en el concepto del cálculo está marcado por los límites. Los límites pueden ser entendidos fácilmente al observar sus propiedades.
Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.
Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.
Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.
Las propiedades de los límites, también conocidas como “Teoremas De Límite Central “, se pueden establecer como:
1). El límite de una función siempre es único y es por esta razón que siempre se refiere a estos como “El Límite” y no simplemente límite. Esta propiedad básica se puede demostrar como:
Si 
y, 
Entonces, L1 = L2
y, Entonces, L1 = L2
2). El límite de la sumatoria de dos funciones es igual a la suma de los límites de las dos funciones por separado.
3). Del mismo modo, el límite de la resta de dos funciones es igual a la resta de los límites de las dos funciones por separado.
4). El caso similar se puede demostrar con la multiplicación, es decir,
5). Para la división, la regla básica es similar a la de la suma y la resta. Sin embargo, en el caso de la división, , esto es, se debe tener cuidado para que el denominador no se convierta en 0 ya que dará lugar a un “error cero”.
6). Una constante que se multiplica con el límite, se puede tomar fuera del límite sin afectar el resultado. Es decir,
7). El límite de un número fijo o inmutable es un número fijo en sí mismo.
8). El límite global de la proporción (cociente) de dos funciones es la proporción del límite de las dos funciones por separado.
9). Límite de la Función Exponencial: De acuerdo a esta propiedad,
10). Límite de una Función Logarítmica: De acuerdo a ella,
11). Teorema de Estricción: Considerando el caso f® g® h® para r acercarse a x .Si
Entonces,
Es decir, la función g® se dice que esta ‘apretada’ entre f ® y g® y que tienen los mismos límites.
Los “Teoremas De Límite Central” también son verdaderos para los límites izquierdos así como para los límites derechos.
La aplicación de las propiedades de los Límites se puede ver en el siguiente ejemplo:
Suponga que el límite de la ecuación 
será encontrado:
será encontrado:
Usando la propiedad del cociente, los límites se pueden aplicar al numerador y al denominador por separado, es decir,
De acuerdo a la 5ta propiedad, la constante se puede tomar fuera del alcance del límite
Luego aplicando la propiedad de la sumatoria y separando los límites en dos límites individuales en el denominador, obtenemos
Por último, aplicando el valor de los límites de la ecuación correspondiente
- See more at: http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites#sthash.Np1KRPUx.dpuf
2.3 Límites laterales
Para que exista el límite de una función, deben existir los límites laterales y coincidir.
El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera
- x ® a- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.
- x ® a+ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.
Límite lateral por izquierda
 si dado e > 0, $ d > 0 tal que
si a - d < x < a Þ
  |
Límite lateral por derecha
 si dado e > 0, $ d > 0 tal que
si a < x < a + d Þ
  |
Observación. Una función tiene límite si los límites laterales son iguales, es decir, cuando 
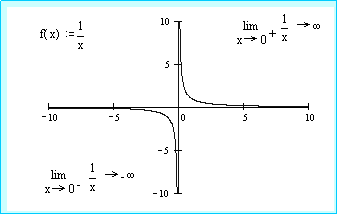
2.4 LIMITES INFINITOS
Decimos que lim f(x)=
si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos.
si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos.
Con rigor, decimos que lim f(x)= si fijado a un valor k positivo y tan grande como se quisiera, existe un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entoces f(x)>k.
si fijado a un valor k positivo y tan grande como se quisiera, existe un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entoces f(x)>k.
Análogamente, lim f(x) = –
x→a
x→a
si para los valores de x cercanos a a, los valores de f(x) se pueden hacer tan pequeños como queramos.
Diremos que lim f(x) = –
x→a
x→a
si fijado un valor de k positivo y tan grande como se quisiera, podemos encontrar un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entonces f(x) < -k
•Ejemplo:
la función f(x)= 1/|x|
En el punto x=0 se tiene:
lim 1/|x| = –
x→ 0-
→ lim 1/|x| = x→0
x→ 0-
→ lim 1/|x| =
x→0
lim 1/|x| =
x→a’
x→a’
||LIMITES AL INFINITO||
cuando el dominio de y= f(x) se extiende indefinidamente hacia la derecha o hacia la izquierda de la recta real tienen sentido las expresiones:
• lim f(x) = L si “haciendo x arbitrariamente grande”, los valores de f(x) se acercan a L.
x→
x→
•lim f(x) = L si “haciendo x arbitrariamente pequeña, los valores de f(x) se acercan a L. x→
2.5 continuidad y descontinuidad
Existen diferentes Tipos de Funciones Discontinuas tales como:
Una función tiene una discontinuidad evitable, en un punto a, si existe límite de la función en el punto, a, pero o no coincide con el valor de la función, f(a), o a no pertenece al dominio de f. Es decir, verifica 2ª pero no se cumple 1º o 3ª.
Ejemplo. La función 
es discontinua en x =3, pues la función no existe en 3, pero sí existe el límite en ese punto (comprobarlo) por lo tanto la discontinuidad es evitable
es discontinua en x =3, pues la función no existe en 3, pero sí existe el límite en ese punto (comprobarlo) por lo tanto la discontinuidad es evitable
Si existen los límites laterales en un punto, pero no coinciden, la discontinuidad se llama de salto. El salto (finito) es la diferencia entre estos valores (en valor absoluto). Cuando uno de los límites laterales de infinito se trata de una discontinuidad de salto infinito.
Ejemplo. a) la función signo 
en x = 0 presenta una discontinuidad de salto 2, pues
en x = 0 presenta una discontinuidad de salto 2, pues
y el salto es 1-(-1)=2.
b) La función f(x) = 1/x es discontinua en 0 de salto infinito.
Si no existe alguno de los límites laterales la discontinuidad se dice de 2ª especie, o esencial.
Ejemplo. 
tiene una discontinuidad esencial en 0.
tiene una discontinuidad esencial en 0.  |
es decir no existen ni los límites laterales pues “oscilan entre 1 y -1”
>>> AQUI UN VIDEO DONDE SE EXPLICA UNA DISCONTINUIDAD<<<
2.6 Aplicaciones a las ciencias económico administrativas: interés compuesto continuamente, límite de la función costo promedio.
INTERÉS COMPUESTO CONTINUO
Un sistema de interés compuesto en el que la capitalización se produce continuamente. Es decir, en el primer instante de tiempo se obtiene interés sobre el principal. Durante el siguiente instante se obtienen intereses sobre el principal incrementado en los intereses que se han ganado durante el instante anterior. Cuando los tipos de interés o los cambios de porcentaje de valor se miden de esta manera, poseen útiles propiedades matemáticas de las que carecen los tipos establecidos con cualquier otra frecuencia compuesta. Por esta razón, los cambios de porcentaje en los trabajos analíticos más avanzados se miden como intereses compuestos continuos.
Aplicaciones en Economía
En la Economía también es importante considerar la variación de una cantidad respecto a otra. Por ejemplo la demanda de un producto respecto a su precio, o el precio de un producto respecto a su costo de producción o la utilidad obtenida en la venta de un producto, con relación al costo de producción, etc.
Por lo anterior, es muy importante la representación de las cantidades relacionadas en forma de funciones que puedan ser derivables, no obstante que los datos que se manejan sean discretos, por ejemplo cuando se establece la función de costo 
, la variable x representa unidades de cierta mercancía.
, la variable x representa unidades de cierta mercancía.
Objetivo
Resolver algunos problemas sencillos en Economía.
Resolver algunos problemas sencillos en Economía.
Conceptos previos
En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedioque expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginalque expresa el cambio instantáneo en una cantidad respecto a la otra.
En Economía se suele describir la variación de una cantidad respecto a otra mediante un concepto llamado promedioque expresa la variación de una cantidad sobre un rango específico de valores de otra y un concepto llamado marginalque expresa el cambio instantáneo en una cantidad respecto a la otra.
Un símil de los conceptos anteriores en Física serían los conceptos de velocidad promedio y velocidad instantánea o lo que geométricamente serían la pendiente de la recta secante y la pendiente de la recta tangente, respectivamente.
- Un ejemplo:
- Si
- El costo promedio de producción de cada unidad, sería el costo total entre la cantidad de unidades de mercancía producidas, es decir:
, a la cual se le llama función del Costo Promedio.
- El costo marginal cuando
es
, si esta cantidad existe. Y se interpreta como la razón de cambio instantánea del Costo Total con respecto al cambio unitario en las unidades producidas, cuando se producen
- De manera similar
sería el Costo Promedio Marginal cuando
- Si
- Otro ejemplo
- Si p es el precio de unitario de cierta mercancía y x el número de unidades de dicha mercancía. Es natural pensar que la cantidad solicitada por los consumidores en el mercado, dependa de su precio. Es natural pensar que "a menor precio, mayor demanda y a mayor precio, menor demanda".
- A veces también es posible considerar que el precio de un producto se puede establecer en función de su demanda: "a mayor demanda menor precio". En este caso, tendríamos p = g(x) que se llamaríafunción de demanda o inclusive podría establecerse mediante una ecuación de demanda. A la gráfica correspondiente que relaciona cantidad x solicitada y el precio p, los economistas acostumbran llamarlecurva de la demanda.
Aquí un caso típico de curva de demanda- Un caso típico: La demanda de un cierto producto es nula cuando el precio es muy alto (p=18), mientras que el consumo máximo de dicho producto en una familia no puede pasar de cierto valor (6 unidades) aun que el precio fuese cero.
- Derivado de estos conceptos, se tiene la función de Ingreso Total, R(x) = x P(x), es decir: la cantidad de unidades vendidadas, por el precio de las mismas.
- Y además la función de Ingreso Marginal, R'(x) = P(x) + x P'(x), que representaría la razón de cambio del ingreso total para cada x.
No hay comentarios:
Publicar un comentario